REDUCED ORDER EXTENDED STATE OBSERVER WITHOUT OUTPUT DERIVATIVE IN ADRC

P. TEPPA-GARRAN^† and G. GARCIA^‡

† Departamento de Procesos y Sistemas, Universidad Simón Bolívar, Valle de Sartenejas, Municipio Baruta, Estado Miranda, Caracas, Venezuela, pteppa@usb.ve

‡ CNRS, LAAS, 7 Avenue du Colonel Roche, F-31400 Toulouse, France and Université de Toulouse, LAAS, INSA, Toulouse, France, garcia@laas.fr

Cite this article as:

Teppa-Garran, P., Garcia, G. (2015) “ REDUCED ORDER EXTENDED STATE OBSERVER WITHOUT OUTPUT DERIVATIVE IN ADRC”, Latin American Applied Research, 45(4) pp 239-244.

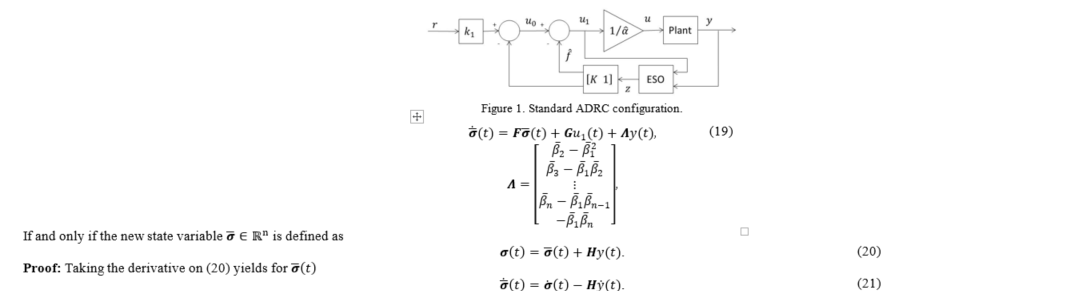
Abstract-- As an observer based method; the ESO in ADRC introduces more phase lag when the observer order becomes higher. The key detriment of phase lag is the reduction of loop stability. A way to decrease the phase lag is to employ a RESO. Nevertheless, the underlying disadvantage of this approach is that RESO computation depends on output derivative. To overcome this problem, the derivative of the output is usually approximated from the difference of two neighbouring output sample values. However, this approach is not convenient for two raisons. First, the use of simple differences to derive the output is another source of phase lag. Second, observers are particularly sensitive to noise and derivative gains amplify noise increasing the sensitivity of the RESO. 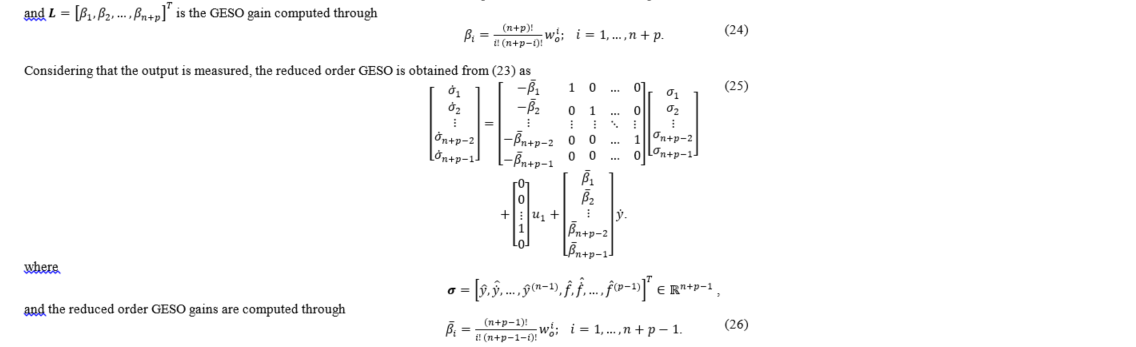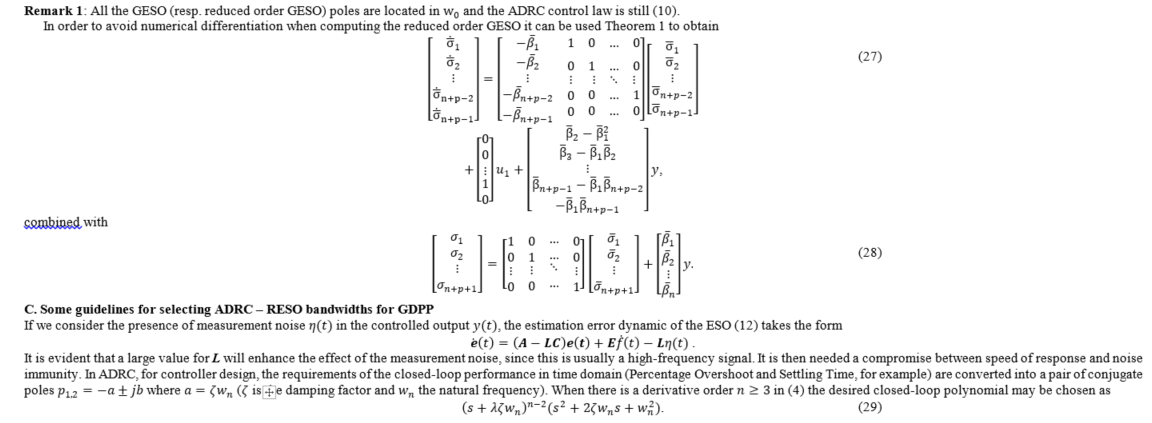In this work, it is employed a method to obtain a RESO that does not depend on the output derivative. It is also developed the reduced order version of the GESO.

Keywords-- Active Disturbance Rejection Control (ADRC), Extended State Observer (ESO), Reduced order ESO (RESO), Generalized ESO (GESO), Measurement noise.

I. INTRODUCTION

ADRC (Gao et al., 2001, Han 1998, 1999, 2009) is a method that does not require a detailed mathematical description of the system. The basic idea is to model the system with an input disturbance that represents any difference between the model and the actual system, including external disturbances, this general disturbance is then estimated in real time and the information is fed back to cancel its effect. One of the main issues in control is to deal with uncertainties including internal (parameter and unmodeled dynamics) and external (disturbances). However, most uncertainties are not measurable. Hence, how to estimate uncertainties by using the control input and output of the system is a significant problem. Many approaches such as, disturbance accommodation control (DAC) (Johnson, 1971, 1976), the unknown input observer (UIO) (Basile and Marro, 1969, Hostetter and Meditch, 1973), the disturbance observer (DOB) (Bickel and Tomizuka, 1999, Profeta et al.1990, Schrijver and Van Dijk, 2002) and the ESO (Gao et al., 2001, Han 1998, 1999, 2009) have been proposed to estimate uncertainties from the input-output data. In DAC, UIO and DOB the external disturbance of a linear time-invariant system is estimated and then rejected. DAC and UIO can be viewed as a special case of DOB (Profeta et al. 1990). The main difference between ESO and DAC, UIO and DOB is that ESO was conceived to deal with nonlinear systems with mixed uncertainties (i.e. unmodeled dynamics and disturbances). The ADRC technique assumes that mixed uncertainties can be considered as one of the states of the system. An estimate of this state, provided by an ESO can be used in the control signal to compensate for the real perturbation in the plant.

As an observer-based method, the ESO in ADRC introduces more phase lag when the observer order becomes higher. The key detriment of phase lag is the reduction of loop stability. A natural and simple way to decrease the phase lag is to employ a reduced order observer. The RESO theory has been proposed in (Tian, 2007) and then applied with success in the control of an induction motor (Zheng et al., 2011), and in different chemical processes (Zheng et al., 2012). Nevertheless, the underlying disadvantage of this approach is that RESO computation depends on output derivative. To overcome this problem, the derivative of the output has been approximated in the existing method from the difference of two neighbouring output sample values. However, this approach is not convenient for two raisons. First, the use of simple differences to find the derivative of the output is another source of phase lag (Ellis, 2002). Second and chiefly from the point of view of this work, in real world implementations, sensor noise is inevitable. Whether caused, for example, by mechanical vibrations in the case of an accelerometer placed on a flexible structure, or caused by quantization of the measured output, in the case of a low-resolution optical encoder, feedback signals contain noise to some extent. Observers’ theory reveals that a trade-off exists between measurement noise sensitivity and the speed of state reconstruction (Kwakernaak and Sivan, 1972). As the observer bandwidth is increased, the presence of noise is exacerbated. The use of derivatives gains produce amplification of the high-frequency signals. These high-frequency signals come from the measurement noise within the system. Hence, the use of derivative outputs can needlessly increase the sensitivity of the observers.

In this work, we employ a state transformation that allows obtaining a RESO that does not depend on the output derivative. In this way, it is avoided intensifying measurement noise and reducing the extra phase lag appearing by direct numerical differentiation on output signal. It is also shown how to extent the developed method to obtain a reduced order version without output derivative of the Generalized Extended State Observer (GESO) proposed by (Miklosovic et al., 2006) to deal with the fast varying generalized perturbation situation in ADR. The article is organized as follows. Section II considers the fundamentals of ADRC in a new general framework. In Section III, it is shown how to avoid the numerical differentiation on the output in the computation of the RESO and the GESO and it is also addressed the theme of how selecting ADRC-RESO bandwidths for guaranteed dominant pole placement (GDPP). Finally, the Section IV shows the effectiveness of the method in a numerical example.

Notation: Matrices and vectors are represented in bold typeface

R is the set of real numbers

V. CONCLUSIONS

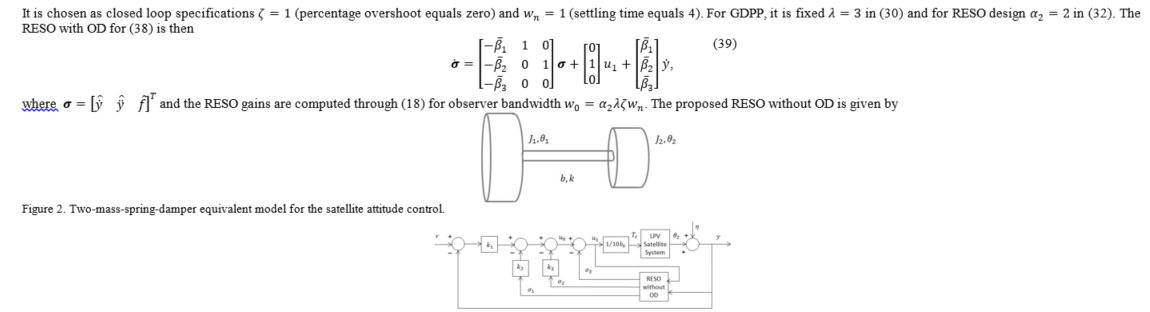
In this work, it has been developed a method within the framework of the ADRC theory to obtain a RESO that does not depend on the output derivative. In this way, it is avoided intensifying measurement noise by direct numerical differentiation on the output signal. One example, the LPV satellite attitude control system, has been employed to test the results and it has been shown that the new approach outperforms the standard RESO method for the example considered. Moreover, it has also been studied how to extent the proposed method to the case of reduced order GESO and in this way it could be possible to treat the situation of fast varying generalized perturbation.

ACKNOWLEDGMENTS

The first author would like to thank the Laboratoire d’Analyse et d’Architecture des Systèmes (LAAS – CNRS) for hosting him during the development of this work.

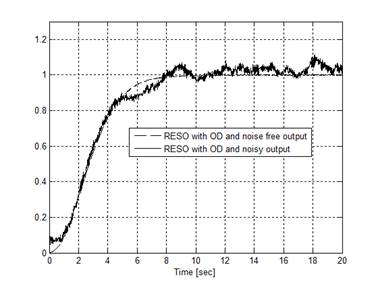
Figure 4. Step set point tracking for RESO with OD.

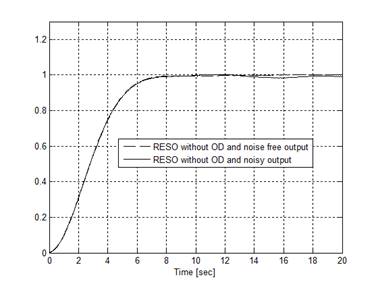
Figure 5. Step set point tracking for RESO without OD.

REFERENCES

Basile, G. and G. Marro, “On the observability of linear, time-invariant systems with unknown inputs” J. of Opt. Th. and Appl., 2, 410-415 (1969).

Bickel, R. and M. Tomizuka, “Passivity-based versus disturbance observer based robot control: equivalence and stability,” ASME J. Dyn. Syst., Meas., and Control, 121, 41-47 (1999).

Ellis, G. Observers in control systems: A practical guide, Academic Press (2002).

Franklin, G., D. Powell and A. Emami-Naeini, Feedback control of dynamic systems, 3^rd edition, Addison Wesley, (1993).

Gao, Z., Y. Huang and J. Han, “An Alternative Paradigm for Control System,” IEEE Conference on Decision and Control, USA, 4578-4585 (2001).

Gao, Z., “Scaling and Bandwidth-Parameterization Based Controller Tuning,” American Control Conference, USA, 4989-4996 (2003).

Han, J., “Auto-Disturbance Rejection Control and its Applications,” Control and Decision, 13,19-23 (1998).

Han, J., “Nonlinear Design Methods for Control Systems,” IFAC World Congress, China (1999).

Han, J., “From PID to active disturbance rejection control,” IEEE Trans. on Indust. Electronics, 56, 900-906 (2009).

Hostetter, G. and J. Meditch, “On the generalization of observers to systems with unmeasurable, unknown inputs,” Automatica, 9, 721-724 (1973).

Johnson, C.D., “Accommodation of External Disturban-ces in Linear Regulator and Servomechanism Problems,” IEEE Trans. Automat. Contr., 16, 635-644 (1971).

Johnson, C.D., “Theory of disturbance-accommodating controllers,” Contr. and Dyn. Syst., 12, 387-489 (1976).

Kwakernaak, H. and R. Sivan, Linear Optimal Control System, Wiley-Interscience (1972).

Miklosovic, R., A. Radke and Z. Gao, “Discrete implementation and generalization of the extended state observer,” American Control Conference, USA, 2209-2214 (2006).

Profeta, J., W. Vogt and M. Mickle, “Disturbance estimation and compensation in linear systems,” IEEE Trans. on Aero. and Electr. Syst., 26, 225-231 (1990).

Schrijver, E. and J. Van Dijk, “Disturbance observers for rigid mechanical systems: Equivalence, stability and design,” ASME J. Dyn. Syst., Meas., and Control, 124, 539-548 (2002).

Tian, G., Reduced-order extended state observer and frequency response analysis. Ph.D. Thesis, Cleveland State University (2007).

Zheng, Q., L. Gao and Z. Gao, “On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamic,” IEEE Conf. Decision Control, 3501-3506 (2007).

Zheng, Q., K. Chedella, W. Xu and L. Wu. “Reduced-order active disturbance rejection control for induction motors,” IEEE International Conference of Control Applications, USA, 1139-1144 (2011).

Zheng, Q., A. Daloum, X. Weifenga and Y. Zheng, “Reduced-order active disturbance rejection control for multivariable chemical processes,” Industry Applications Society Annual Meeting, 1-7 (2012).

Received: October 28, 2013.

Accepted: March 20, 2015.

Recommended by Subject Editor: Jorge Solsona.